En las últimas dos entradas introducimos la ecuación de la conducción del calor según la forma
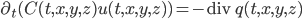 .
.
Para que esta forma resulte en una ecuación cerrada para la temperatura es necesario dar relaciones fenomenológicas tanto de la capacidad calorífica del terreno como del flujo de calor en términos de la temperatura. Sólo de este modo será posible analizar matemáticamente la ecuación para interpretar distintos sistemas geotérmicos.
La temperatura es algo tan fundamental en la naturaleza que prácticamente cualquier propiedad depende de ella, y la capacidad calorífica de un material no es una excepción. Sin embargo, se da el caso que en muchas situaciones prácticas en las que el rango de temperaturas está acotado (no son ni muy muy frías ni muy muy calientes), la capacidad calorífica es esencialmente independiente de la temperatura. En estas situaciones es habitual tomar el valor de  como constante (respecto el tiempo). Evidentemente, si en el sistema hay otros procesos que pueden influir en la capacidad calorífica del terreno, como cambios en la humedad relativa, entonces se requerirán relaciones que vinculen tales procesos con la variable
como constante (respecto el tiempo). Evidentemente, si en el sistema hay otros procesos que pueden influir en la capacidad calorífica del terreno, como cambios en la humedad relativa, entonces se requerirán relaciones que vinculen tales procesos con la variable  , pero estos escenarios quedan más allá de la dinámica térmica propiamente dicha.
, pero estos escenarios quedan más allá de la dinámica térmica propiamente dicha.
A diferencia de la capacidad calorífica, el flujo de calor está íntimamente relacionado con el perfil de temperaturas en el terreno. De hecho, parte de la relación que hay entre estas dos variables se deriva de la segunda ley de la termodinámica, según la cual la temperatura fluye de focos cálidos a focos fríos (siempre que no se ejerza trabajo sobre el sistema para revertir esta tendencia, como en las bombas de calor por ejemplo). Esta ley implica que el flujo de calor, que es un vector ya que el flujo tiene una magnitud (cantidad de energía que fluye) y una dirección (hacia donde se mueve la energía), tiene que apuntar hacia la dirección de máxima pendiente descendiente del perfil de temperaturas, tal y como se muestra en la siguiente figura (nótese que hemos obviado la variable espacial 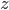 para poder representar oportunamente la gráfica de la función
para poder representar oportunamente la gráfica de la función 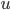 ):
):

Matemáticamente, el gradiente de una función en un punto apunta hacia la dirección de máximo pendiente ascendente sobre la gráfica de la función en dicho punto. La magnitud (la norma) del vector gradiente coincide con dicho pendiente: cuanto mayor es la norma del vector gradiente mayor es el pendiente de la función. Por lo tanto, decir que el vector 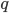 apunta en la dirección de máximo pendiente descendiente de la gráfica de
apunta en la dirección de máximo pendiente descendiente de la gráfica de 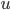 es decir que
es decir que 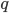 es proporcional a
es proporcional a  (donde la letra griega
(donde la letra griega  indica el operador gradiente, es decir
indica el operador gradiente, es decir 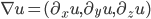 ). Más concretamente, podemos expresar el flujo de calor como
). Más concretamente, podemos expresar el flujo de calor como
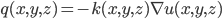
donde 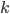 , que debe tomar valores positivos, representa la conductividad térmica del terreno en el punto
, que debe tomar valores positivos, representa la conductividad térmica del terreno en el punto 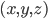 . En la ecuación anterior es esclarecedor interpretar
. En la ecuación anterior es esclarecedor interpretar  como la derivada de la temperatura en la dirección del flujo de calor. En general, la conductividad podría depender de la temperatura e incluso de su gradiente, es decir
como la derivada de la temperatura en la dirección del flujo de calor. En general, la conductividad podría depender de la temperatura e incluso de su gradiente, es decir 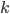 podría tomar la forma
podría tomar la forma 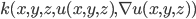 . Afortunadamente, en la mayoría de casos prácticos es realista suponer que
. Afortunadamente, en la mayoría de casos prácticos es realista suponer que 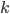 depende sólo del tipo de material por dónde fluye el calor, y es suficiente considerar
depende sólo del tipo de material por dónde fluye el calor, y es suficiente considerar  como en la ecuación anterior. Es oportuno observar también que, en particular, si el terreno es relativamente homogéneo, entonces la conductividad es la misma en todos los puntos, y en este caso
como en la ecuación anterior. Es oportuno observar también que, en particular, si el terreno es relativamente homogéneo, entonces la conductividad es la misma en todos los puntos, y en este caso 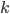 es constante respecto las variables espaciales. La relación descrita en la ecuación anterior es lo que se conoce como ley de Fourier, ya que fue el matemático francés Joseph Fourier quién introdujo esta relación y desarrollo gran parte de la matemáticas que se usan actualmente para analizar la dinámica del calor (y por extensión muchas otras ecuaciones en derivadas parciales). Fue un pionero.
es constante respecto las variables espaciales. La relación descrita en la ecuación anterior es lo que se conoce como ley de Fourier, ya que fue el matemático francés Joseph Fourier quién introdujo esta relación y desarrollo gran parte de la matemáticas que se usan actualmente para analizar la dinámica del calor (y por extensión muchas otras ecuaciones en derivadas parciales). Fue un pionero.

Combinando las relaciones anteriores para  y para
y para 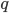 , la ecuación cerrada que describe la conducción del calor es
, la ecuación cerrada que describe la conducción del calor es
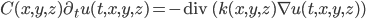 .
.
Ahora ya sí que disponemos de la herramienta fundamental para modelizar y analizar distintos sistemas geotérmicos. En el primer sistema supondremos que tenemos un depósito enterrado que intercambia calor con el suelo, pero esto ya será en la siguiente entrega!
Carles Barril