En la última entrada de esta sección presentamos la ecuación
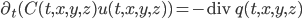
dónde 
representa la capacidad térmica del terreno y 
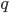es el vector de flujo de la energía calorífica. A primera vista, no es evidente que esta ecuación tenga nada que ver con la conducción del calor. Para entender un poco más la lógica que se esconde detrás suyo, es oportuno proceder de la siguiente forma. Primero debemos imaginar que queremos calcular la variación de energía calorífica en un cubo pequeño de terreno, como el de la figura siguiente.
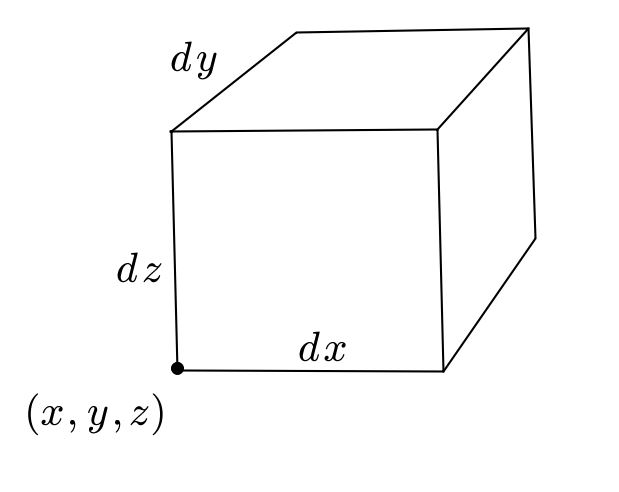
Esta región se traduce, matemáticamente, en un conjunto de puntos. La energía calorífica que hay en esta región se obtiene, por tanto, “sumando” la energía calorífica que hay almacenada en cada uno de sus puntos. La palabra sumar en la frase anterior es un tanto delicada. El problema es que un punto del espacio es algo tan pequeño que no puede almacenar energía alguna. Una forma de ver esto es recordando que la capacidad térmica de un material es la energía calorífica almacenada por grado de temperatura y unidad de volumen, y puesto que el volumen de un punto es cero, cero debe ser la energía que almacena. Observemos también que, de no ser así, si los puntos pudieran almacenar cierta energía, entonces habría una cantidad infinita de energía en cualquier volumen puesto que en cualquier volumen hay siempre una infinidad de puntos. Los problemas energéticos de la humanidad dejarían de existir! Volviendo a la tierra después de este detour por las idealizaciones matemáticas, cuando digo que “sumamos” la energía que hay en cada punto lo que realmente quiero decir es que la integramos. Esto es, la energía calorífica almacenada en el cubo es
.
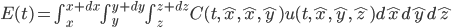Como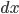 
, 
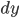y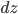 
son suficientemente pequeños,
la integral de la derecha puede aproximarse como
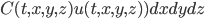
de modo que la
variación de esta cantidad de energía no es más que su derivada temporal,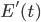 
. En particular, la variación de
energía en el punto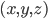 
por unidad de tiempo y volumen es
,
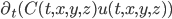como era de esperar si se tiene en cuenta la definición de y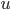 
.
Por otro lado, la
variación de la cantidad de energía también se puede calcular integrando el
balance energético del flujo de calor que entra y sale del cubo. La energía que
entra por la cara más a la izquierda (perpendicular al eje de las 
)
es, aproximadamente (de nuevo la aproximación es tanto mejor como más pequeños
sean 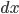, 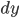y ),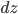
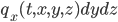
y la que sale por la cara más a la derecha (también perpendicular al eje de las ) es, aproximadamente,
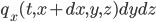
de modo que el
balance energético en la dirección de las se puede aproximar como
.
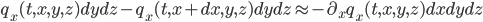De forma análoga
se tiene que los balances en las direcciones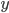 
y 
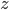son,
aproximadamente,
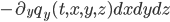
y
.
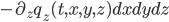El balance total en el cubo es la suma de estos tres balances, de modo que la variación de energía en el cubo es (usando la definición de la divergencia de un campo vectorial)
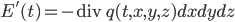
En particular, siguiendo este procedimiento obtenemos que la variación de energía en el punto 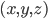por unidad de tiempo y volumen es
,
de modo que
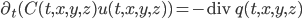
como queríamos ver!
Bufff! Me ha quedado mucho más denso de lo que quería. Y eso que he sacrificado cierto rigor matemático para hacer la exposición más clara. Bueno, la siguiente entrega será más relajada.
Carles Barril