Esta sección pretende introducir y desarrollar algunos de los modelos que se usan en geotermia. Los modelos son aproximaciones de la realidad que sirven para calcular la cantidad de calor que se puede extraer del subsuelo a lo largo del tiempo. El ingrediente clave que hay detrás de estos modelos es la Ecuación del Calor (qué casualidad, no?), una entidad que tiene nombre propio por su relevancia en distintos campos de la ciencia, desde la probabilidad a la biología de poblaciones, pasando claro está por la termodinámica. La presencia de esta ecuación en áreas tan distintas se debe a que lo que realmente modeliza la Ecuación del Calor es la difusión de alguna “cosa”. En el caso de la geotermia esta “cosa” es la energía calorífica, en biología de poblaciones se trata de individuos, y en probabilidad la “cosa” que difunde es algo tan abstracto como la densidad de probabilidad de un suceso. En cualquier caso, cuando el francés Joseph Fourier planteó la ecuación por primera vez a principios del siglo XIX, lo hizo centrándose en la difusión del calor por conducción, de ahí el nombre. Y ahora sí, sin más dilación, una primera versión de la ecuación
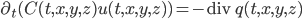
donde 
es una función que indica la capacidad térmica del terreno, es decir la cantidad de energía almacenada en el terreno por cada grado y unidad de volumen (sus unidades son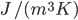 
), la función 
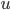representa la temperatura y 
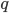es el vector de flujo de la energía calorífica. Todas estas funciones pueden depender tanto del punto del terreno 
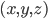como del instante temporal 
.
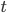Próximamente veremos como se deduce la ecuación anterior y veremos cómo generalizarla para incorporar fuentes y sumideros de calor. También hablaremos de la ley de Fourier que relaciona el vector 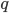con la función 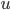. En este punto ya tendremos una de las herramientas más importantes para afrontar los problemas (¡matemáticos!) de la geotermia.
Carles Barril